Number system in hindi:-
आज हम number system के बारें में पढेंगे तथा ये कितने प्रकार के होते है ये सब जानेंगे तो चलिए शुरू करते है.
number system का प्रयोग सूचना को प्रदर्शित करने के लिए किया जाता है.. जब भी हम कोई letters या word कंप्यूटर में लिखते है तो वह उसे number में बदल देता है क्योंकि कंप्यूटर केवल numbers को समझता है.
डिजिटल कंप्यूटर, सभी प्रकार का डेटा तथा सूचना बाइनरी संख्या में प्रदर्शित करता है. जैसे:- ऑडियो, विडियो, ग्राफ़िक्स तथा संख्या आदि.
number system निम्नलिखित चार प्रकार के होते है:-
1:- decimal number system
2:- binary number system
3:- octal number system
4:- hexadecimal number system
1:- decimal number system (डेसीमल नंबर सिस्टम):-
डेसीमल नंबर सिस्टम का प्रयोग हम अपनी दैनिक जीवन में करते है. जिसमें किसी भी संख्या को प्रदर्शित करने के लिए 0, 1, 2, 3, 4, 5, 6, 7, 8, तथा 9 अंक प्रयोग किये जाते है.
इस number system का आधार (base or radix) 10 है. radix किसी नंबर सिस्टम में प्रयोग किये जाने वाले अंकों की संख्या होती है.
decimal number system में लिखी गयी प्रत्येक संख्या के प्रत्येक अंक का अपना एक स्थानीय मान (weight) होता है. इसे गुणक (multiplying factor) भी कहते है.
गुणक हजार, सैकड़ा, दहाई तथा इकाई इत्यादि होते है.
उदाहरण के लिए-
6262.67 को निम्नलिखित प्रकार से प्रदर्शित किया जा सकता है.
(6262.67)10 = 6*103+2*102+6*101+2*100+6*10-1+6*10-2
इस उदाहरण में 6 को 103 से गुणा किया गया है , 2 को 102 से गुणा किया गया है, 6 को 101 से गुणा किया गया है. तथा 2 को 100 से गुणा किया गया है. इसी तरह इसके दशमलव वाले भाग में 6 को 1/101 अर्थात 10-1 से तथा 7 को 1/102 अर्थात 10-2 से गुणा किया गया है.
2:- binary number system (बाइनरी नंबर सिस्टम):-
digital computer अपना सारा डेटा बाइनरी नंबर में ही प्रदर्शित करते है. बाइनरी सिस्टम में केवल दो नंबर 0 तथा 1 प्रयोग किये जाते है तथा इसका आधार (base or radix) 2 है. क्योंकि इसमें केवल दो digits होती है.
उदाहरण के लिए:- 1100110, एक बाइनरी संख्या है क्योंकि इसमें केवल 0 तथा 1 अंक का ही प्रयोग किया गया है, 1001001.1101 भी एक बाइनरी संख्या है. इसमें 1001001 के बाद लगा बिंदु(.) binary point कहलाता है.
3:- octal number system (ऑक्टल नंबर सिस्टम):-
octal number system में केवल 8 अंक 0 से 7 तक होते है. ये 8 अंक 0, 1, 2, 3, 4, 5, 6, तथा 7 होते है.
इस संख्या प्रणाली का आधार (base or radix) 8 है.
4:- hexadecimal number system (हेक्साडेसीमल नंबर सिस्टम):-
hexadecimal number system में 10 अंक तथा 6 letters होते है;- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
इसमें 10 को A के द्वारा, 11 को B के द्वारा, 12 को C के द्वारा, 13 को D के द्वारा. 14 को E के द्वारा तथा 15 को F के द्वारा प्रदर्शित किया जाता है.
इसका आधार (base or radix) 16 है क्योंकि इसमें 16 alphanumeric वैल्यू है.
TABLE FOR DIFFERENT NUMBER SYSTEM:-
Number system conversions in hindi:-
number system को बदलने के निम्नलिखित प्रकार होते है:-
- बाइनरी से डेसीमल
- डेसीमल से बाइनरी
- ऑक्टल से डेसीमल
- डेसीमल से ऑक्टल
- ऑक्टल से बाइनरी
- बाइनरी से ऑक्टल
- हेक्साडेसीमल से बाइनरी
- बाइनरी से हेक्साडेसीमल
- हेक्साडेसीमल से डेसीमल
- डेसीमल से हेक्साडेसीमल
- ऑक्टल से हेक्साडेसीमल
- हेक्साडेसीमल से ऑक्टल
1:- binary to decimal conversion (बाइनरी से डेसीमल में बदलना):-
इसको निम्नलिखित प्रकार किया जाता है:-
(110110)2 = 1*25+ 1*24+ 0*23+ 1*22 +1*21 +0*20
= 32+ 16+ 0+ 4+ 2
= (54)10
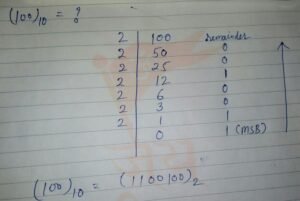
2:- decimal to binary conversion (डेसीमल को बाइनरी में बदलना):-
डेसीमल संख्या को बाइनरी में बदलने के लिए संख्या को 2 से लगातार भाग किया जाता है तथा प्रत्येक division के बाद remainder को रिकॉर्ड किया जाता है.
अंतिम बाइनरी result के लिए सभी remainders को उलटे क्रम में लिखते है. इस क्रम में पहला अंक MSB तथा अंतिम अंक LSB होता है.
3:- octal to decimal (ऑक्टल को डेसीमल में बदलना):-
(324)8 = 3*82 + 2*81 + 4*80
= 3*64 + 2*8 + 4*1
= 192+ 16+ 4
= (212)10
4:- decimal to octal (डेसीमल को ऑक्टल में बदलना)
5:- octal to binary conversion (ऑक्टल को बाइनरी में बदलना):-
ऑक्टल को बाइनरी में बदलने के लिए प्रत्येक ऑक्टल अंक के स्थान पर उसके EQUIVALENT 3 बिट बाइनरी संख्या लिखी जाती है.
6:- binary to octal conversion:-
7:- hexadecimal to binary:-
हेक्साडेसीमल को बाइनरी में बदलने के लिए हेक्स संख्या का प्रत्येक अंक उसके 4 बिट बाइनरी EQUIVALENT में लिखा जाता है.
